Kirchhoff’s Voltage Law (KVL)

The algebraic sum of the voltage drops in any closed path in a circuit and the electromotive forces in that path are equal to zero. In traveling around a closed path, we encounter various voltages, some of which carry a positive sign while others carry a negative sign in the algebraic sum.

  • A convenient convention is to use the first polarity mark encountered for each voltage to decide if it should be added or subtracted in the algebraic sum.

  • If we go through the voltage from the negative polarity reference to the positive reference, it carries a minus sign.

  • If the polarity marks are encountered in the opposite direction (plus to minus), the voltage carries a negative sign.


    For the circuit of Figure 8.2, we obtain the following equations:
 (8.2)

 

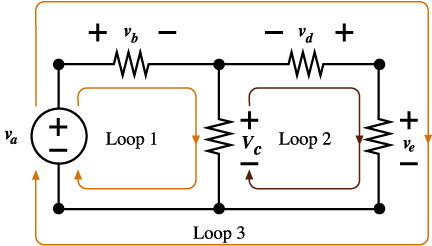
Figure 8.2 Circuit showing three closed paths to illustrate Kirchhoff’s
                  Voltage Law (KVL).

KVL may be applied to a simple closed-loop circuit taking into account the following guidelines:

  1. For a voltage source, the assumed loop current flow from – to + is considered positive and is given the + sign.

  2. For a voltage source, the assumed loop current flow from + to - is considered negative and is given the - sign.

  3. The direction of the assumed loop current is always positive. Therefore, the current enters the resistance from the positive side and leaves from the negative side.

  4. The polarity of a voltage source is not changed by the direction of the assumed loop current.
               

Content and Pedagogy© 2004, University of Ottawa, Faculty of Engineering and Faculty of Education
Design and Production © 2004, University of Ottawa, Centre for e-Learning