Exercise

What is the current, voltage, and power for each element of the circuit shown in Figure 11.2?

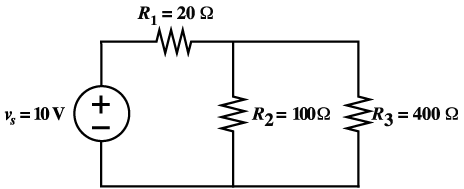
Figure 11.2 Circuit diagram of series-parallel resistors.

Type your solution in the box below:

Solution:

First combine the two resistances (R₂ and R₃) in parallel to obtain the following circuit.



Replacing R₂ and R₃ by their parallel equivalent, we obtain the circuit shown in Figure 11.3



Figure 11.3 Circuit after replacing R₂ and R₃ with R_T1.


Notice that R₁ and R_T1 are in series. Let’s replace these resistances by their equivalent (sum) R_T as shown in the circuit in Figure 11.4.





Figure 11.4 Circuit after replacing R₁ and R_T1by their equivalent R_T


After reducing the circuit to an equivalent resistance and a source, we may apply Ohm’s law to find the current through the equivalent resistance.

(11.1)

We know that this current flows downward (from plus to minus) through R_T. This means that the current 0.1 A flows clockwise around the circuit.

Because R_T is the equivalent resistance seen by the source in all three parts of Figure 11.5, the current through V must be i₁= 0.1 A flowing upward in all three equivalent circuits.



Figure 11.5 Circuit


Look at the circuit shown in Figure 11.6 to realize that the current i₁ flows through the source vs and the equivalent resistance R_T1. The voltage across R_T1 can be found by applying Ohm’s law again

(11.2)

Figure 11.6 Circuit


Since R_T1 is the equivalent resistance for the parallel combination of R₂ and R₃, the voltage v₂ appears across both R₂ and R₃in Figure 11.6.

(11.3)

As a check, apply KCL to verify that i ₁ = i₂ + i₃. Also we can apply Ohm’s law to calculate v₁

(11.4)

As a check, apply KVL to verify that v _s = v₁ + v₂.

Now, we compute the power for each element. For the voltage source v_s, we have

(11.5)

We have included the minus sign because the references for v_sand i₁ are opposite to the passive configuration. Since the power for the source is negative, this means that the source is supplying energy to the other elements in the circuit.

The powers for the resistors are

(11.6)

As a check, we verify that p_s + p₁ + p₂ + p₃ = 0, showing that power is conserved.