CSI-5174 - Assignment 4: Protocol design - - SOLUTION

Given: November 9 - - Due: Noember 21 - - This will only count for 10 points - the purpose is to prepare yourself for some questions in the final exam that may be related to these topics

Question 1: Use Gouda's method to design a protocol between two components that exchange messages over a reliable medium

Property X: The protocol should have the property that the two components are always in corresponding states when no message is in transit

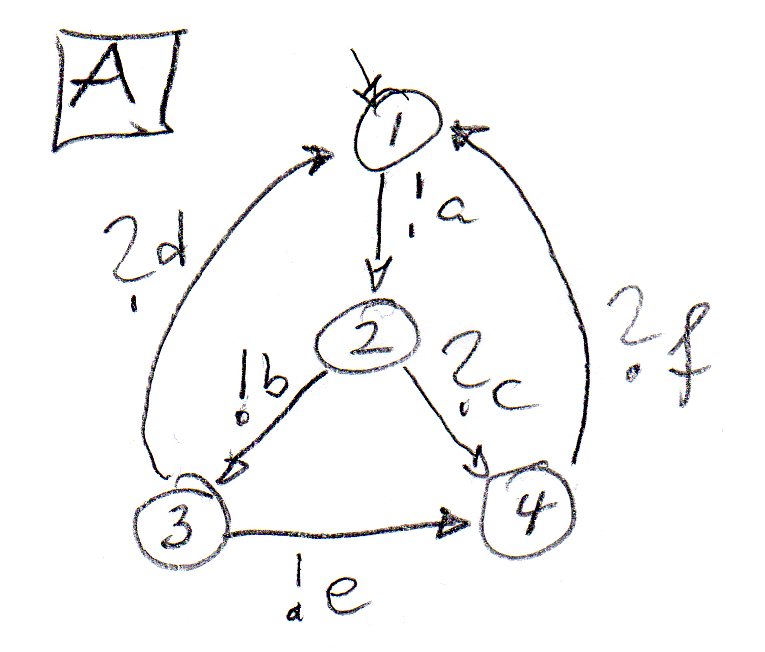
The basic behavior of component A is given by the following state machine. The basic behavior of component B is obtained from the behavior of A by complementing inputs and outputs. These basic behaviors must be complemented to obtain a protocol without unspecified receptions such that the property X is satisfied.

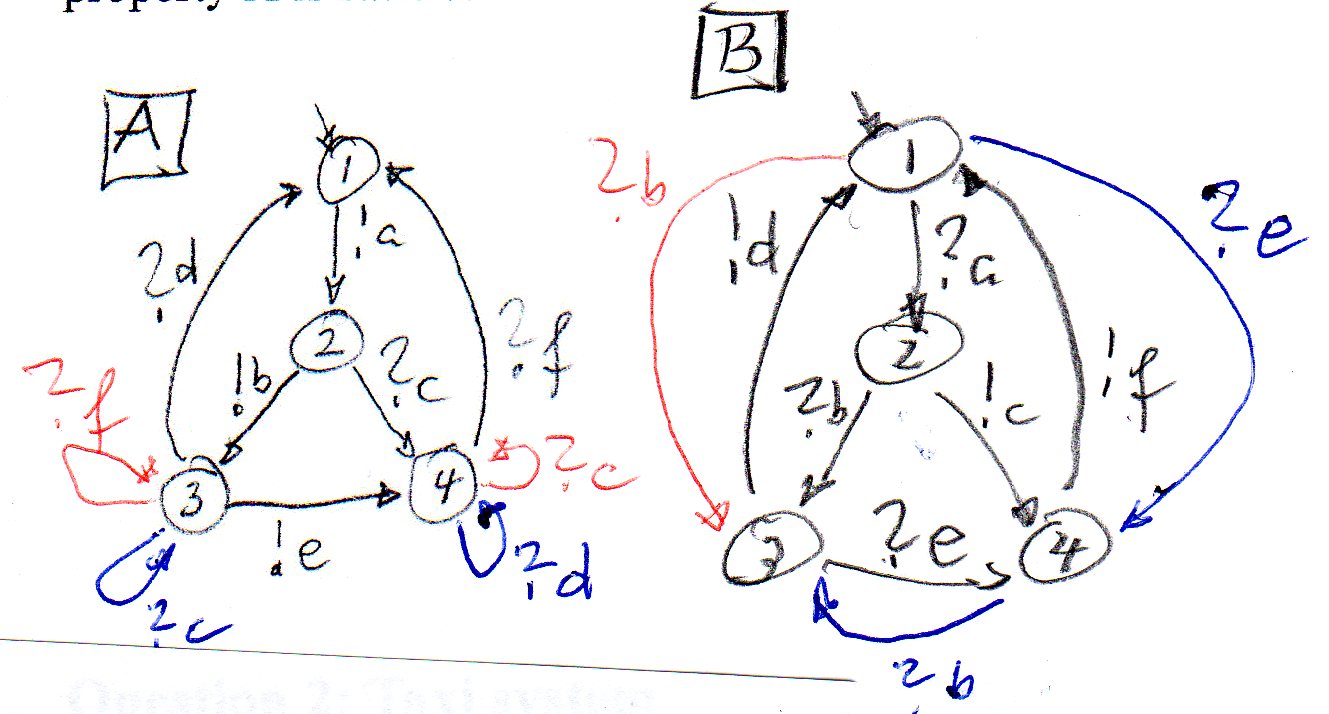
The basic behavior of B is shown below in black. We follow Gouda"s method and give priority to A. There are two mixed states, 2 and 3. If we assume that in state 2, A produces the output b ane B produces the output c, we get unspecified receptions which can be resolved by additional transitions in A and B, respectively (b received in state 4 and c received in state 3). This is shown in blue below. Similarly, simultaneous sending from state 3 (messages e nd d) also gives rise to unspecified receptions which can be resolved by corresponding receptions (also shown in blue below).

This example has additional difficulties: A, after sending b could immediately send e, and if B sends simultaneously c, this c can also be received by A in state 4. Also B may send immediately after c an f. This means that A may receive an f in state 3 (after the reception of the c). And the b sent by A may be received by B in state 1 (in which case B should go into state 3, because A has priority). This nedessary additional adjustments are shown in red in the figures below.

Question 2: Taxi system

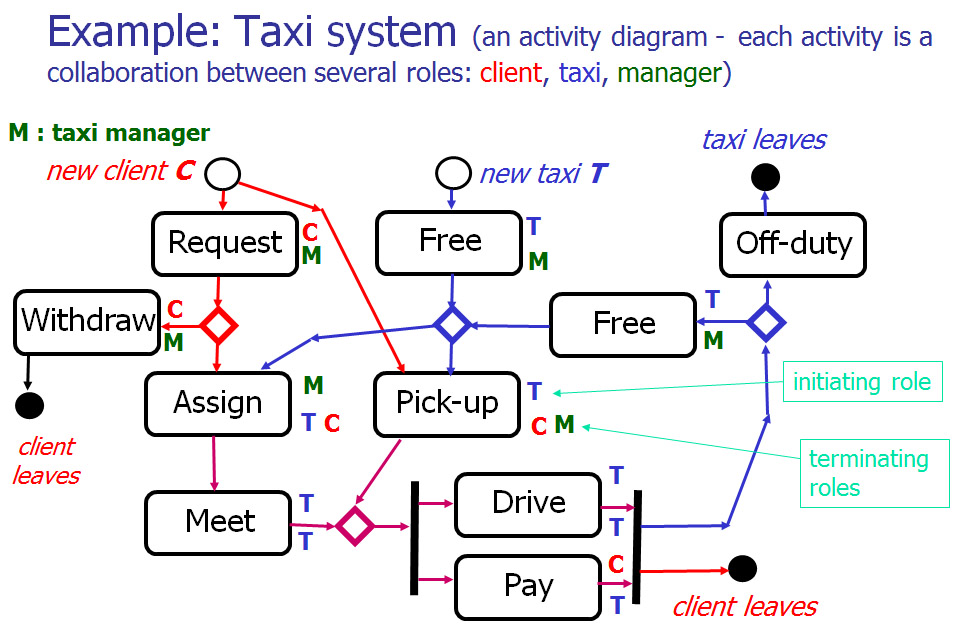
We consider the taxi system described in the course notes. We assume that all sequencing between the different activities shown as arrows in the diagram are weak sequences. There are several cases of non-local choices (competing initiatives).

Part 1: Ignoring the competing initiatives (assuming that never both sides would take an initiative), use the protocol derivation approach described in the course notes to derive state machine behaviors for the three components: user, taxi and manager. You may assume that the system contains only one user, one taxi and one manager.

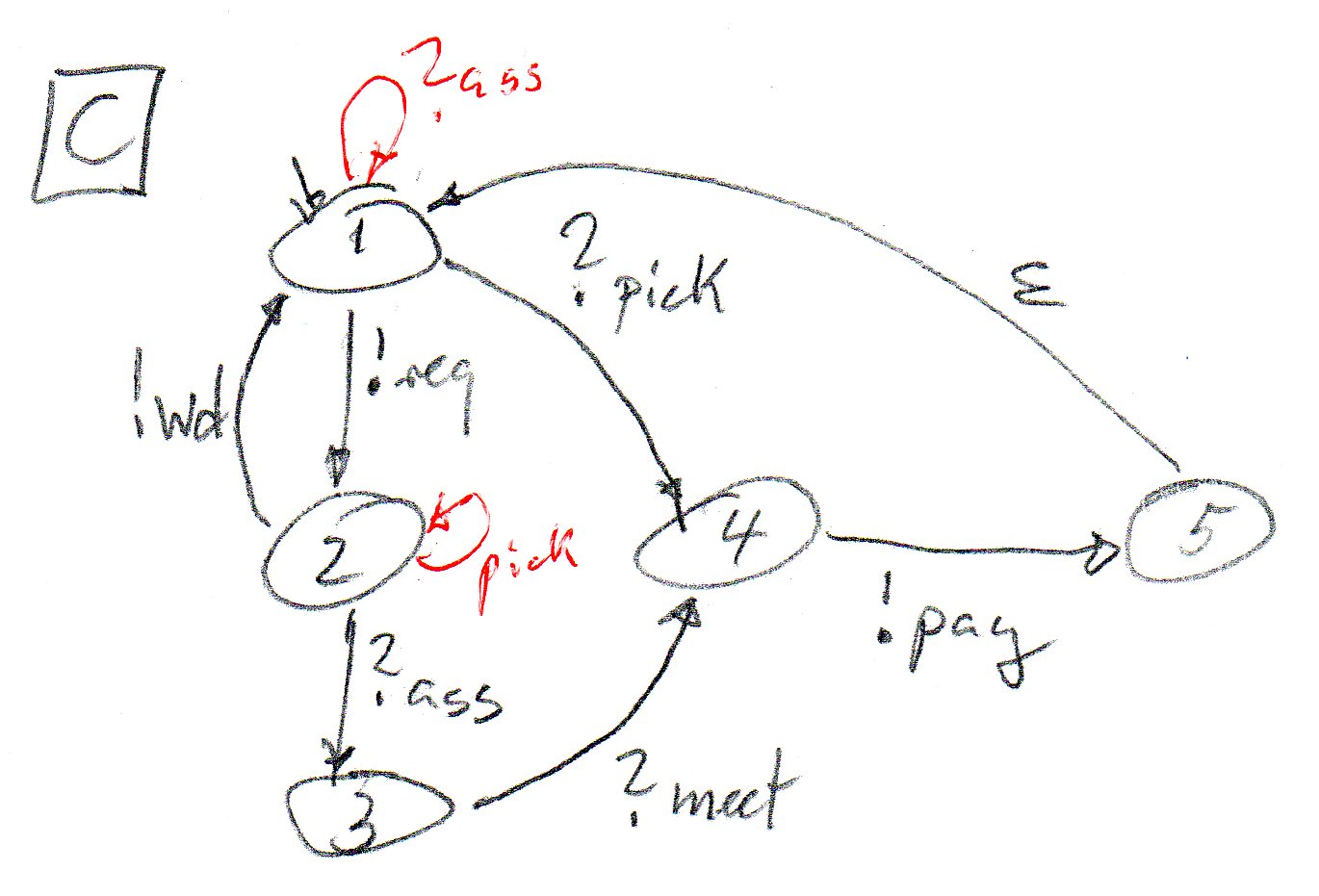
The figure below pm the left is the specification of the taxi system as given in the course notes. I have first rewritten this specification in terms of an LTS (see figure to the right). It assumes that there is one client and one taxi, and that the taxi is initially in the free state. I have indicated (as in the figure to the left) what is the initiating component (upper index) and what are the other components involved (lower index). It is assumed that each LTS transition represents the exchange of one of more messages, as indicated in the cours notes. Notes:

• In contrast to the original specification, the diagram on the right assumes that the Meet action also involves the client, and the Pick-up operation also involves the taxi (in the diagram from the course notes, the lower index represent the terminating components, not all participating components).
• The transition from state 4 to state 5 corresponds to the parallel execution of the Drive and Pay operations.

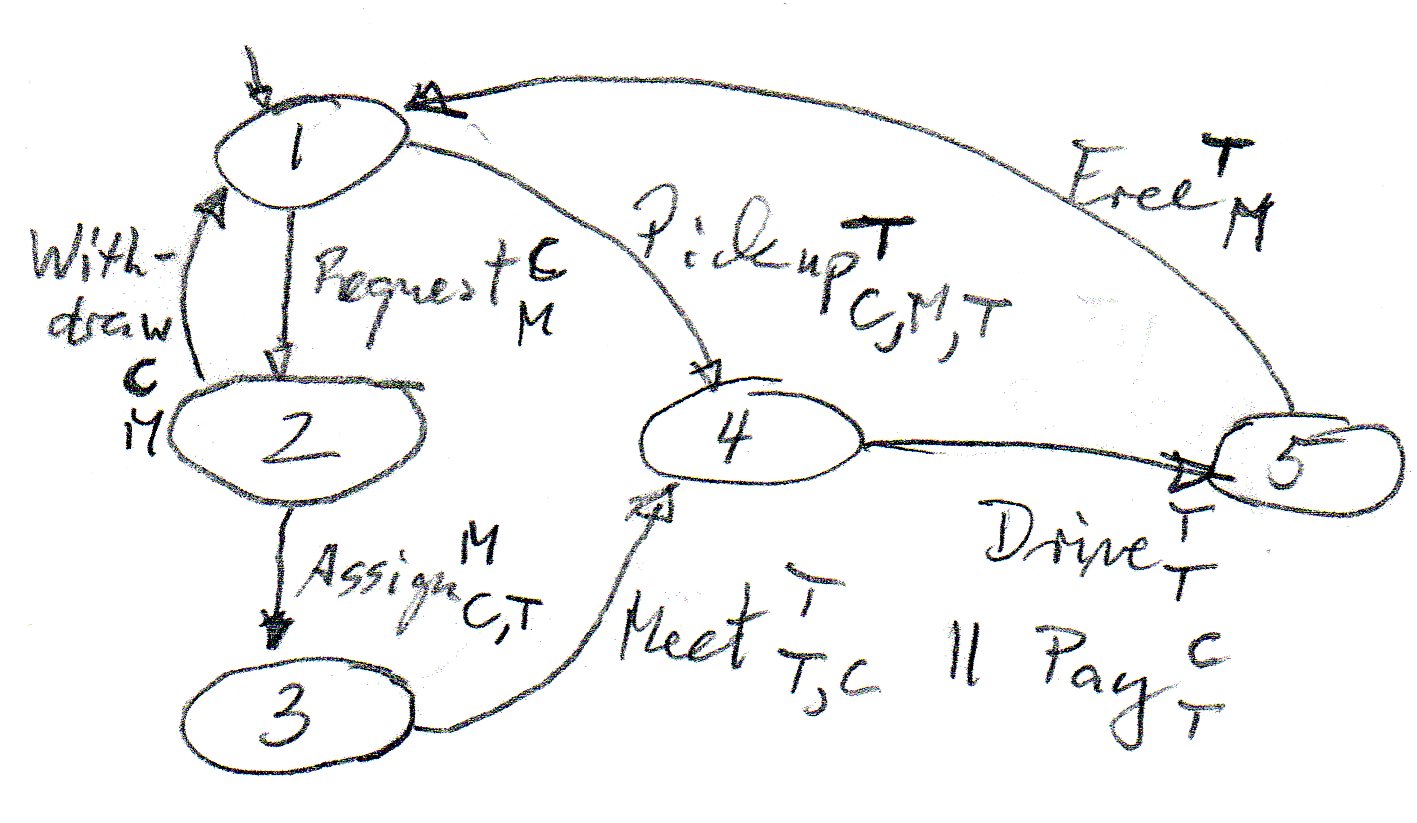
From the diagram on the right, I have then derived the component behaviors shown by the diagrams below (the black part only). Here the operations of the upper diagram on the right are replaced by the reception or sending of messages (with corresponding names). The component initiating an operation sends the corresponding message (possibly to two partners) and the other components receive the message. For the Assign and Pick-up operations, two messages are sent - they are sent in parallel (the destination is indicated as lower index). For the messages sent to a single component, the destination is not explicitly given, but can be deduced by looking which component has the corresponding reception. Notes:

• If some component is not involved in an operation, I have indicated a spontaneous transition (labelled epsilon). For instance, the client could go directly from state 4 to state 1 after the pay message is sent. I have left state 5 in the specification in order to show the similarity with the upper right diagram.
• However, in the state machine for the Taxi, I have eliminated state 2, because there is a choice in state 1 between the Pick-up and Assign operations.

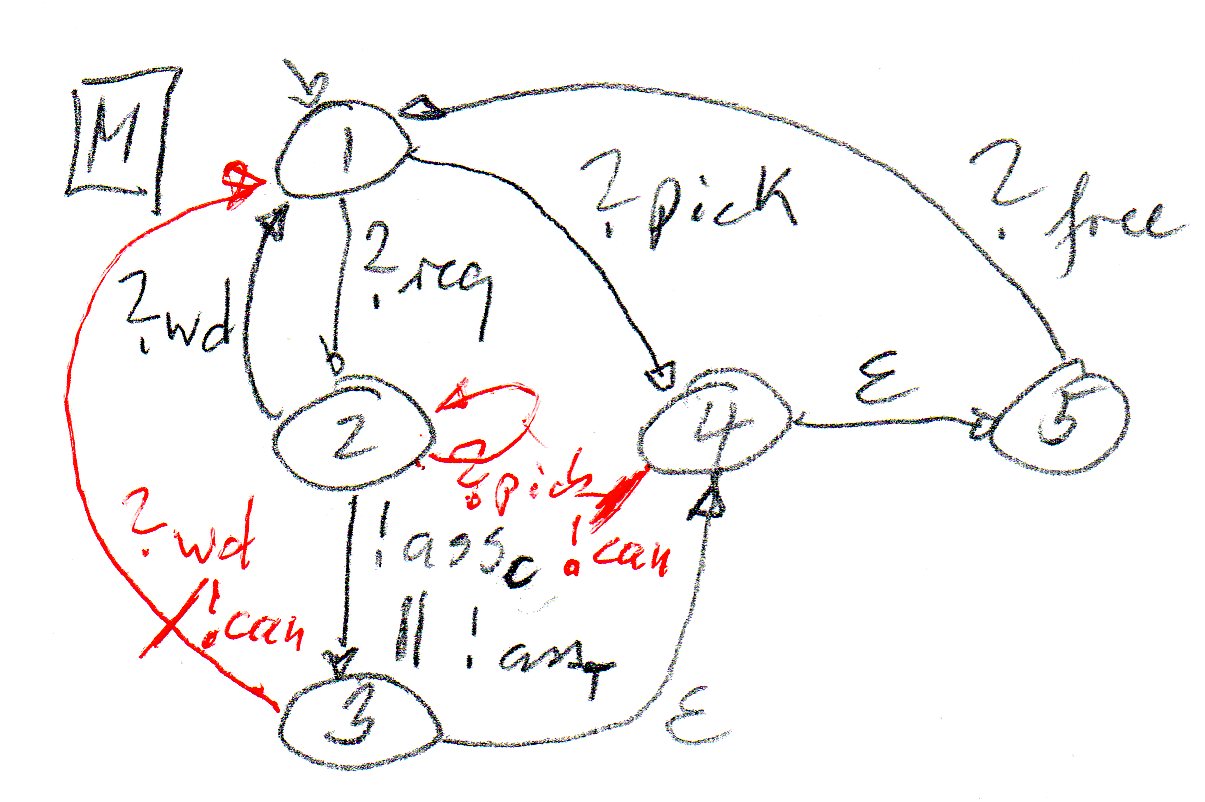
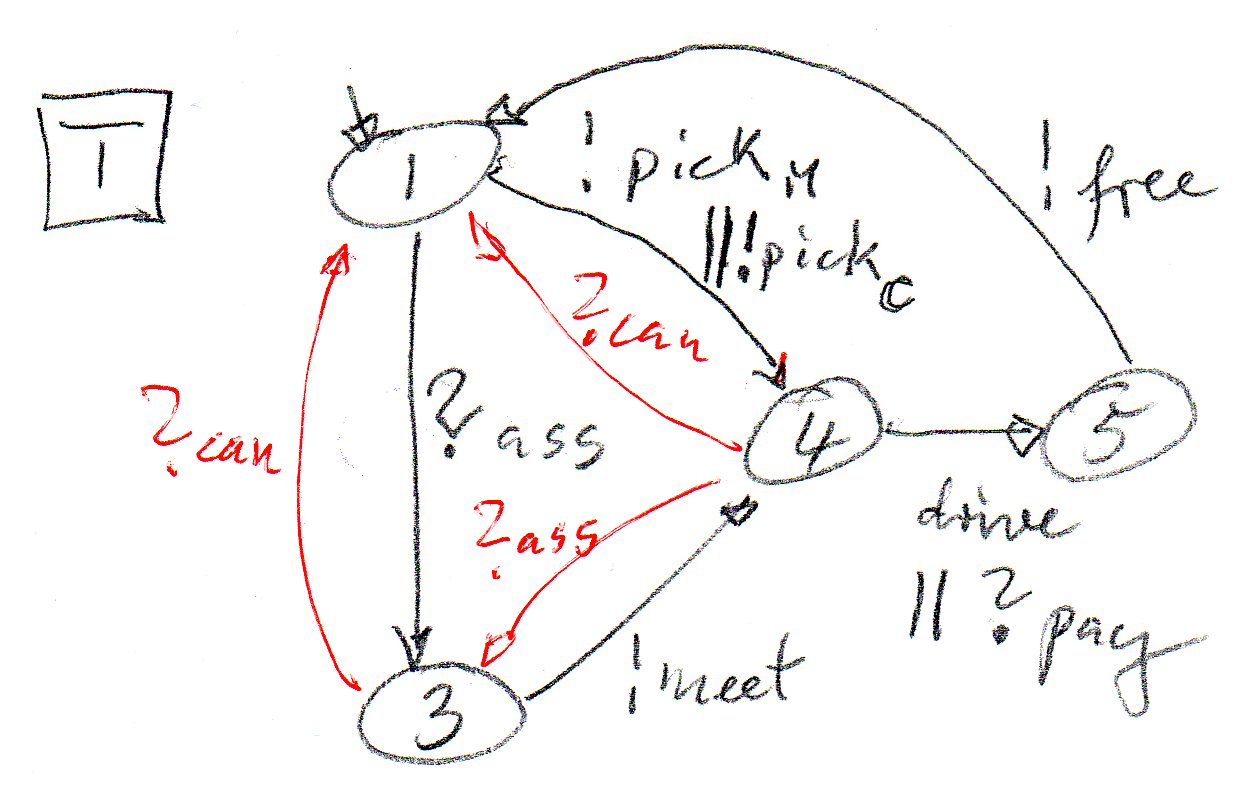
Part 2: Check the protocol obtained for Part 1 for unspecified receptions (note: each non-local choice would give rise to unspecified receptions) - you may do this intuitively or by performing reachability analysis. Identify the non-local choices.

It is clear from the above diagrams that the states 1 and 2 are mixed states.

Part 3: Use Gouda's method to resolve the non-local choices by adding suitable reception transitions. Does the obtained system work without problems ?

If we assume that the client has priority in both of these mixed state, the situation is somehow more complicated than discussed in the Gouda paper, since we have here 3 components, not only two. I have come up with a design for the three components as shown in the three diagrams above (including the red transitions). This may not be a complete solution; I am not sure whether I have made any errors (sorry, I did not make a reachability analysis for my proposed solution in order to check its correctness). Here is a short explanation.

• For the mixed state 2, the conflict is between the client and the manager. Gouda's method gives rise to the ?wd transition of the manager and the ?ass transition of the client. However, when the client withdraws when the manager is already in state 3, the taxi should also be informed about this fact. Therefore I have included in the ?wd transition the action of sending a cancel (can) message to the taxi, which would be received in state 3.
  • However, the taxi could already be in state 4. Therefore the reception of the can message is also foreseen in this state.
• For the mixed state 1, the conflict is between the client and the taxi. Gouda's method gives rise to the ?pick transition in the client. Then I have introduced the ?pick/!can transition in the manager which cancels the Pick-up when the message is received in state 2. This cancel message would be received by the taxi in state 4.

This example shows you that sometimes the standard methods (like Gouda's method for two components in the case of this example) are not sufficient for the problem at hand. It is important to be inventive and come up with solutions to the problems by modifying and extending what you have learned.